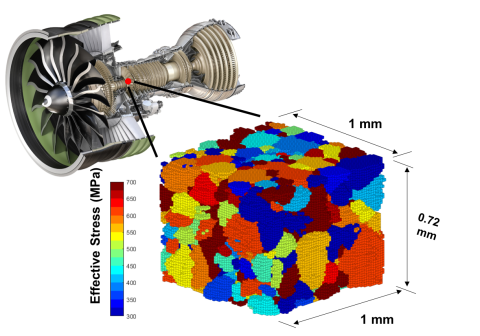
Understanding stress is crucial for safe, efficient mechanical designs. Both SMB and FAST beamlines can can perform stress measurements during applied loading and as residual stresses both at the crystalline aggregate and individual crystal size scales. InSitµ helps to understand residual stress, allowing designers to move away from over-conservative, heavier approximations, paving the way to light-weighting materials.
Understanding Stress in Materials
X-rays have been used for interrogation and characterization of structural materials for a century. The discoveries behind x-ray diffraction and the overarching principles that basically enabled the field of modern crystallography are all based on the fundamental relationships that exist between diffracted x-ray intensity and the underlying material structure. The tremendous utility of x-ray diffraction experiments is the ability to utilize a diffraction model to convert a collection of diffracted x-ray intensity into a quantitative, often geometric description of the material structure that produced it. A high energy synchrotron light source produces well-characterized, concentrated beams of monochromatic high energy (short wavelength) x-rays that are capable of penetrating through bulk metallic samples during high energy x-ray diffraction (HEXD) experiments. Capturing large patterns of diffracted x-rays is now possible using modern area detectors with increasingly fast (sub-second) detection times and ever smaller pixel size. By employing ancillary equipment that can precisely control external loads, temperature and other environmental conditions, diffraction patterns can be obtained in real time in situ from a test specimen subjected to conditions that closely approximate those experienced during processing or in service.
Accurate representation of the evolving geometry of a multi-dimensional domain and the accompanying approximation of spatially-varying fields over that domain are the hallmarks of the finite element method (FEM), as is the ability to specify the relevant conditions on the boundary of a domain and the manner in which those conditions vary with time. The basic premise of the FEM is the discretization of the domain into elements and the representation of each field variable (such as stress, velocity or temperature) within each element using a decomposition into shape or interpolation functions of the spatial variables (ie. x,y,z) and the nodal point values of the field variable. While FEM is typically thought of as an engineering tool for designing structures or representing fluid flows and temperature fields, the great promise of finite elements for fundamental material science is this ability to systematically approximate the time-varying topology of a deforming material and at several relevant size scales, the values of important mechanical field variables such as stress, lattice orientation and strain rate.